Parallel ILU
ViennaCL provides implementations of parallel incomplete LU and parallel incomplete Cholesky factorization preconditioners with static pattern for CUDA, OpenCL, and OpenMP. The underlying algorithms have been proposed by Chow and Patel in their paper Fine-Grained Parallel Incomplete LU Factorization. While the paper only presents results for CPUs and Xeon Phis, the implementation in ViennaCL also support CUDA and OpenCL to support all major hardware platforms.
In the following we compare the performance of a sequential ILU0 preconditioner with the parallel ILU preconditioner as proposed by Chow and Patel. Finite element discretizations of the Poisson equation on the unit square and unit cube for triangular/tetrahedral grids generated with Netgen are considered as our benchmark problem. BiCGStab was used as Krylov solver. Total solver time to reach a relative reduction of the residual of nine orders of magnitude were recorded.
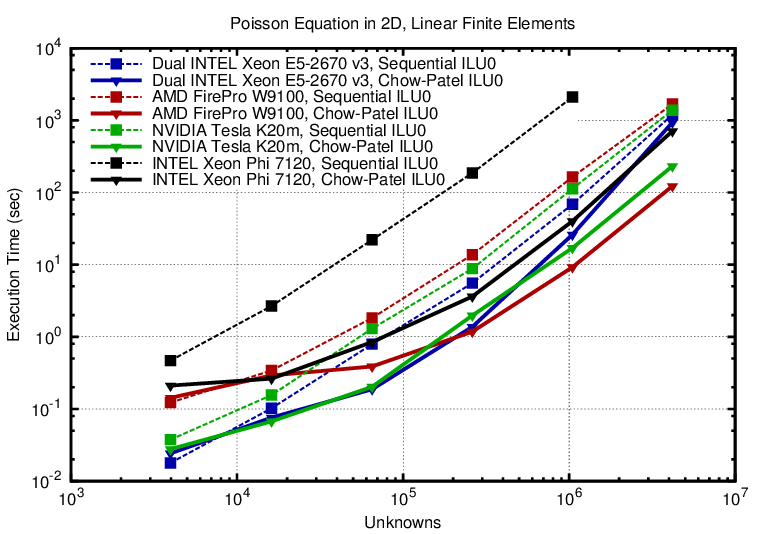
Performance gains of the parallel ILU over the conventional ILU0 preconditioner are observed to be about one order of magnitude across the dual-socket Xeon CPUs, the NVIDIA K20m, and the AMD W9100. The savings on the Xeon Phi are almost two orders of magnitude, because the Xeon Phi offers only very low sequential performance.
Note that the graphs also show that ILU is not a good scalable preconditioner: The total time to solution grows faster as the number of unknowns, so for large problem sizes it is worthwhile to consider alternatives with better asymptotic behavior, for example Algebraic Multigrid.

The benchmark for the three-dimensional Poisson equation leads to similar results: Performance gains of about one order of magnitude are obtained on the NVIDIA and AMD GPUs, whereas the savings on the Xeon Phi are almost two orders of magnitude. The Xeon CPUs show performance gains of about a factor of three. This lower performance gain can be explained by a good fraction of the available memory bandwidth being accessible for single-threaded execution.





