Algebraic Multigrid
ViennaCL provides implementations of algebraic multigrid (AMG) preconditioners for CUDA, OpenCL, and OpenMP. The implementations are based on the techniques presented by [Bell et al.] and implemented for CUDA in the CUSP library. ViennaCL's extension of these ideas to OpenMP and OpenCL allows for a much broader coverage of hardware available.
The highly optimized pipelined preconditioners in ViennaCL with iterative solvers using algebraic multigrid preconditioners are compared on different high-end hardware in the following. Finite element discretizations of the Poisson equation on the unit square and unit cube for triangular/tetrahedral grids generated with Netgen are considered. A-priori one expects AMG to exhibit the best asymptotic behavior, while the unpreconditioned pipelined solvers are likely to be faster for smaller system sizes. This is confirmed by the results for the 2D case:
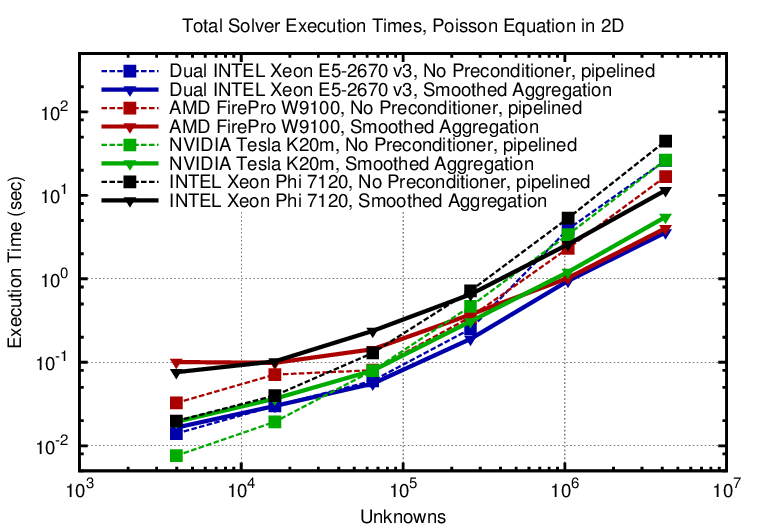
The smoothed aggregation AMG (other variants are also available) indeed outperforms the unpreconditioned solver for large system sizes. The best performance is obtained on the dual-socket Haswell system, mostly because of the faster sparse matrix-matrix products. The AMD FirePro W9100 and the NVIDIA K20m show similar performance, even though the the AMD GPU suffers from fairly high kernel launch overheads at smaller system sizes. The Xeon Phi (KNC) falls behind the other hardware platforms by about a factor of three.
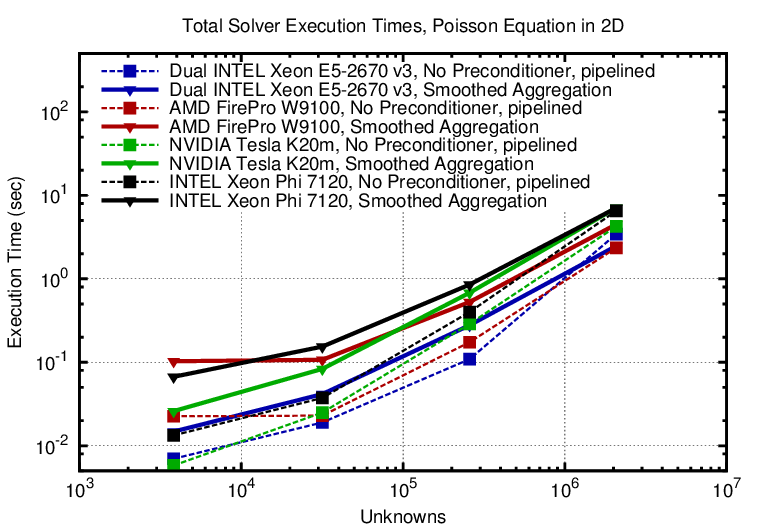
In the 3D case the unpreconditioned iterative solvers are the better pick in terms of time-to-solution for system sizes below one million unknowns. However, for more complicated systems this may no longer be the case (higher iteration counts or even divergence).





