About ViennaCL
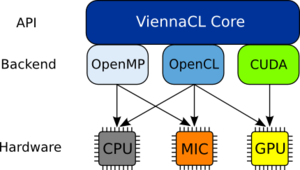
The Vienna Computing Library (ViennaCL) is a free open-source scientific computing library written in C++ and provides CUDA, OpenCL and OpenMP computing backends. It enables simple, high-level access to the vast computing resources available on parallel architectures such as GPUs and is primarily focused on common linear algebra operations (BLAS levels 1, 2 and 3) and the solution of large systems of equations by means of iterative methods with optional preconditioners.
Core Features
All core features are considered mature and available on all computing backends.
- Convenient C++ API for common dense and sparse linear algebra operations
- BLAS levels 1, 2 and 3 supported
- Multiple compute backends: CUDA, OpenCL, and OpenMP
- Vector and matrix proxies for convenient manipulation of subvectors and submatrices
- Three iterative solvers: Conjugate Gradient (CG), Stabilized Bi-Conjugate Gradient (BiCGStab) and Generalized Minimum Residual (GMRES)
- Cholesky preconditioner, (Block-) Incomplete LU preconditioner with threshold (ILU0) or static pattern (ILUT) and optional level scheduling
- Jacobi and row normalization preconditioner
- Interface similar to Boost.uBLAS
- Iterative solvers can also be used directly for uBLAS, Eigen and MTL4 objects
- Convenient data transfer from and to STL, uBLAS, Eigen and MTL4 objects
- Lanczos method and Power Iteration for eigenvalue computation
- QR factorization (used e.g. for least-squares problems)
- Header-only library
- MIT (X11) open source license
- MATLAB interface for iterative solvers (as separate download)
Additional Features
Additional features are only available on some computing backends. Also, interface changes might still occur in the process of features becoming core functionality.
- OpenCL kernel generator from high-level expressions
- Singular value decomposition and nonnegative matrix factorization (both experimental)
- Algebraic Multigrid and sparse approximate inverse preconditioner (both experimental)
- Fast Fourier transform (experimental)
- Structured matrix types for efficient operations: Circulant, Hankel, Toeplitz, Vandermonde (experimental)
- Reordering algorithms for sparse systems of linear equations: Cuthill-McKee, Gibbs-Poole-Stockmeyer (both experimental)
- Multi-device OpenCL support
- ViennaCL can be used with user-provided OpenCL contexts
- Automated OpenCL performance tuning environment available