The implementations of the algorithms described in this chapter are still not yet mature enough to be considered core-functionality, and/or are available with the OpenCL backend only.
In addition to the Preconditioners available in the ViennaCL core, two more preconditioners are available with the OpenCL backend and are described in the following.
An alternative construction of a preconditioner for a sparse system matrix 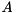 is to compute a matrix
is to compute a matrix 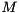 with a prescribed sparsity pattern such that
with a prescribed sparsity pattern such that
![\[ \Vert AM - I \Vert_F \rightarrow \min \ , \]](form_3.png)
where 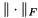 denotes the Frobenius norm. This is the basic idea of sparse approximate inverse (SPAI) preconditioner. It becomes increasingly attractive because of their inherent high degree of parallelism, since the minimization problem can be solved independently for each column of
denotes the Frobenius norm. This is the basic idea of sparse approximate inverse (SPAI) preconditioner. It becomes increasingly attractive because of their inherent high degree of parallelism, since the minimization problem can be solved independently for each column of 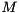 . ViennaCL provides two preconditioners of this family: The first is the classical SPAI algorithm as described by Grote and Huckle [16] , the second is the factored SPAI (FSPAI) for symmetric matrices as proposed by Huckle [17] .
. ViennaCL provides two preconditioners of this family: The first is the classical SPAI algorithm as described by Grote and Huckle [16] , the second is the factored SPAI (FSPAI) for symmetric matrices as proposed by Huckle [17] .
SPAI can be employed for a CPU matrix A of type MatrixType as follows:
The first parameter denotes the residual norm threshold for the full matrix, the second parameter the maximum number of pattern updates, and the third parameter is the threshold for the residual of each minimization problem.
For GPU-matrices, only parts of the setup phase are computed on the CPU, because compute-intensive tasks can be carried out on the GPU:
The GPUMatrixType is typically a viennacl::compressed_matrix type.
For symmetric matrices, FSPAI can be used with the conjugate gradient solver:
Our experience is that FSPAI is typically more efficient than SPAI when applied to the same matrix, both in computational effort and in terms of convergence acceleration of the iterative solvers.
Note that FSPAI depends on the ordering of the unknowns, thus bandwidth reduction algorithms may be employed first, cf. Bandwidth Reduction.
Several routines for computing the eigenvalues of symmetric tridiagonal as well as dense matrices are provided with ViennaCL. The following routines are available for one or two compute backends, hence they are not considered to be part of the core. Also, use the implementations with care: Even though the routines pass the respective tests, they are not as extensively tested as core functionality.
The bisection method for finding the eigenvalues of a symmetric tridiagonal matrix has been implemented within the CUDA SDK as an example. ViennaCL provides an extension of the implementation also suitable for eigenvalues with multiplicity higher than one. In addition, our implementation is not limited to CUDA and also available for OpenCL.
The interface in ViennaCL takes STL vectors as inputs, holding the diagonal and the sub/superdiagonal. The third argument is the vector to be overwritten with the computed eigenvalues. A sample code snippet is as follows:
The return value bResult is false if an error occurred, and true otherwise. Note that the sub/superdiagonal array superdiagonal is required to have an value of zero at index zero (indicating an element outside the matrix).
examples/tutorial/bisect.cpp.The bisection method allows for a fast computation of eigenvalues, but it does not compute eigenvectors directly. If eigenvectors are needed, the tql2-version of the QL algorithm as described in the Algol procedures can be used.
The interface to the routine tql2() is as follows: The first argument is a dense ViennaCL matrix. The second and third argument are STL vectors representing the diagonal and the sub/superdiagonal, respectively. Thus, a minimal code example for a 20-by-20 tridiagonal matrix is as follows:
Note that the sub/superdiagonal array e is required to have an value of zero at index zero (indicating an element outside the matrix).
examples/tutorial/tql2.cpp.Symmetric dense real-valued matrices have real-valued eigenvalues, hence the current lack of complex arithmetic in ViennaCL is not limiting. An implementation of the QR method for the symmetric case for computing eigenvalues and eigenvectors is provided.
The current implementation of the QR method for symmetric dense matrices in ViennaCL takes three parameters:
A minimal example is as follows:
examples/tutorial/qr_method.cpp.Since there is no standardized complex type in OpenCL at the time of the release of ViennaCL, vectors need to be set up with real- and imaginary part before computing a fast Fourier transform (FFT). In order to store complex numbers 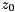 ,
, 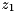 , etc. in a
, etc. in a viennacl::vector, say v, the real and imaginary parts are mapped to even and odd entries of v respectively: v[0] = Real(z_0), v[1] = Imag(z_0), v[2] = Real(z_1), v[3] = Imag(z_1), etc.
The FFT of v can then be computed either by writing to a second vector output or by directly writing the result to v
Conversely, the inverse FFT is computed as
The second option for computing the FFT is with Bluestein algorithm. Currently, the implementation supports only input sizes less than 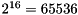 . The Bluestein algorithm uses at least three-times more additional memory than another algorithms, but should be fast for any size of data. As with any efficient FFT algorithm, the sequential implementation has a complexity of
. The Bluestein algorithm uses at least three-times more additional memory than another algorithms, but should be fast for any size of data. As with any efficient FFT algorithm, the sequential implementation has a complexity of 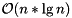 . To compute the FFT with the Bluestein algorithm from a complex vector
. To compute the FFT with the Bluestein algorithm from a complex vector v and store the result in a vector output, one uses the code
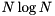 is only computed for vectors with a size of a power of two. For other vector sizes, a standard discrete Fourier transform with complexity
is only computed for vectors with a size of a power of two. For other vector sizes, a standard discrete Fourier transform with complexity 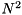 is employed. This is subject to change in future versions.
is employed. This is subject to change in future versions.Some of the FFT functions are also suitable for matrices and can be computed in 2D. The computation of an FFT for objects of type viennacl::matrix, say mat, require that even entries are real parts and odd entries are imaginary parts of complex numbers. In order to store complex numbers 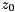 ,
, 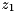 , etc.~in
, etc.~in mat: mat(0,0) = Real(z_0), mat(0,1) = Imag(z_0),mat(0,2) = Real(z_0), mat(0,3) = Imag(z_0) etc.
Than user can compute FFT either by writing to a second matrix output or by directly writing the result to mat
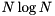 is computed for matrices with a number of rows and columns a power of two only. For other matrix sizes, a standard discrete Fourier transform with complexity
is computed for matrices with a number of rows and columns a power of two only. For other matrix sizes, a standard discrete Fourier transform with complexity 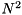 is employed. This is subject to change in future versions.
is employed. This is subject to change in future versions.There are two additional functions to calculate the convolution of two vectors. It expresses the amount of overlap of one function represented by vector v as it is shifted over another function represented by vector u. Formerly a convolution is defined by the integral
![\[ (v*u)(t) = \int_{-\infty}^\infty f(x)g(t-x) dx \]](form_11.png)
Define 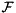 as the Fast Fourier Transform operator, there holds for a convolution of two infinite sequences
as the Fast Fourier Transform operator, there holds for a convolution of two infinite sequences v and u
![\[ \mathcal{F}\{v*u\} = \mathcal{F}\{u\} \mathcal{F}\{v\} \rightarrow v*u = \mathcal{F}^{-1}\{ \mathcal{F}\{v\} \mathcal{F}\{u\} \} \]](form_13.png)
To compute the convolution of two complex vectors v and u, where the result will be stored in output, one can use
which does not modify the input. If a modification of the input vectors is acceptable,
can be used, reducing the overall memory requirements.
Multiplication of two complex vectors u, v where the result will be stored in output, is provided by
For creating a complex vector v from a real vector u with suitable sizes (size = v.size() / 2), use
Conversely, computing a real vector v from a complex vector u with length size = v.size() / 2 is achieved through
To reverse a vector v inplace, use
The singular decomposition of a real-valued matrix 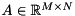 is a decomposition of the form
is a decomposition of the form
![\[ A = U \Sigma V^T \]](form_121.png)
where 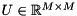 is a unitary matrix holding the left-singular vectors,
is a unitary matrix holding the left-singular vectors, 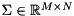 holds the singular values of
holds the singular values of 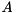 on the diagonal, and
on the diagonal, and 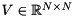 holds the right-singular vectors of
holds the right-singular vectors of 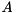 . The singular vectors are stored column-wise in both
. The singular vectors are stored column-wise in both 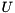 and
and 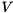 .
.
ViennaCL provides an implementation of the SVD method based on bidiagonalization and QR methods with shift. The API of the svd() routine takes three parameters:
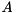 , which gets overwritten with
, which gets overwritten with 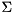 ,
,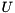 for the left-singular vectors,
for the left-singular vectors,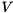 for the right-singular vectors.
for the right-singular vectors.A minimal example is as follows:
tests/src/svd.cpp for an example.The bandwidth of a sparse matrix is defined as the maximum difference of the indices of nonzero entries in a row, taken over all rows. A low bandwidth may allows for the use of efficient banded matrix solvers instead of iterative solvers. Moreover, better cache utilization as well as lower fill-in in LU-factorization based algorithms can be expected.
For a given sparse matrix with large bandwidth, ViennaCL provides routines for renumbering the unknowns such that the reordered system matrix shows much smaller bandwidth. Typical applications stem from the discretization of partial differential equations by means of the finite element or the finite difference method. The algorithms employed are as follows:
The iterated Cuthill-McKee algorithm applies the classical Cuthill-McKee algorithm to different starting nodes with small, but not necessarily minimal degree as root node into account. While this iterated application is more expensive in times of execution times, it may lead to better results than the classical Cuthill-McKee algorithm. A parameter ![$ a \in [0,1] $](form_14.png) controls the number of nodes considered: All nodes with degree
controls the number of nodes considered: All nodes with degree 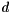 fulfilling
fulfilling
![\[ d_{\min} \leq d \leq d_{\min} + a(d_{\max} - d_{\min}) \]](form_16.png)
are considered, where 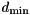 and
and 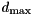 are the miminum and maximum nodal degrees in the graph. A second parameter
are the miminum and maximum nodal degrees in the graph. A second parameter gmax specifies the number of additional root nodes considered.
The algorithms are called for a matrix A of a type compatible with std::vector< std::map<int, double> > by
and return the permutation array. In ViennaCL, the user then needs to manually reorder the sparse matrix based on the permutation array. Example code can be found in examples/tutorial/bandwidth-reduction.cpp.
In various fields such as text mining, a matrix V needs to be factored into factors W and H with the property that all three matrices have no negative elements, such that the function
![\[ f(W, H) = \Vert V - WH \Vert_{\mathrm{F}}^2 \]](form_19.png)
is minimized. This can be achieved using the algorithm proposed by Lee and Seoung [19] with the following code:
The fourth and last parameter to the function nmf() is an object of type viennacl::linalg::nmf_config containing all necessary parameters of NMF routine:
eps_: Relative tolerance for convergencestagnation_eps_: Relative tolerance for the stagnation checkmax_iters_: Maximum number of iterations for the NMF algorithmiters_: The number of iterations of the last NMF run using this configuration objectprint_relative_error_: Flag specifying whether the relative tolerance should be printed in each iterationcheck_after_steps_: Number of steps after which the convergence of NMF should be checked (again)Multiple tests can be found in file viennacl/test/src/nmf.cpp and tutorial in file viennacl/examples/tutorial/nmf.cpp