This tutorial explains how to use the iterative solvers in ViennaCL in a matrix-free manner, i.e. without explicitly assembling a matrix.
We consider the solution of the Poisson equation 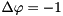 on the unit square
on the unit square ![$ [0,1] \times [0,1] $](form_139.png) with homogeneous Dirichlet boundary conditions using a finite-difference discretization. A
with homogeneous Dirichlet boundary conditions using a finite-difference discretization. A 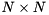 grid is used, where the first and the last points per dimensions represent the boundary. For simplicity we only consider the host-backend here. Have a look at custom-kernels.hpp and custom-cuda.cu on how to use custom kernels in such a matrix-free setting.
grid is used, where the first and the last points per dimensions represent the boundary. For simplicity we only consider the host-backend here. Have a look at custom-kernels.hpp and custom-cuda.cu on how to use custom kernels in such a matrix-free setting.
- Note
- matrix-free.cpp and matrix-free.cu are identical, the latter being required for compilation using CUDA nvcc
We start with including the necessary system headers:
ViennaCL imposes two type requirements on a user-provided operator to compute y = prod(A, x) for the iterative solvers:
- A member function
apply(), taking two ViennaCL base vectors x and y as arguments. This member function carries out the action of the matrix to the vector.
- A member function
size1() returning the length of the result vectors. Keep in mind that you can always wrap your existing classes accordingly to fit ViennaCL's interface requirements.
We define a simple class for dealing with the 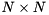 grid for solving Poisson's equation. It only holds the number of grid points per coordinate direction and implements the
grid for solving Poisson's equation. It only holds the number of grid points per coordinate direction and implements the apply() and size1() routines. Depending on whether the host, OpenCL, or CUDA is used for the computation, the respective implementation is called. We skip the details for now and discuss (and implement) them at the end of this tutorial.
template<typename NumericT>
class MyOperator
{
public:
MyOperator(std::size_t N) : N_(N) {}
{
#if defined(VIENNACL_WITH_CUDA)
apply_cuda(x, y);
#endif
#if defined(VIENNACL_WITH_OPENCL)
apply_opencl(x, y);
#endif
apply_host(x, y);
}
std::size_t
size1()
const {
return N_ * N_; }
private:
#if defined(VIENNACL_WITH_CUDA)
#endif
#if defined(VIENNACL_WITH_OPENCL)
#endif
std::size_t N_;
};
Main Program
In the main() routine we create the right hand side vector, instantiate the operator, and then call the solver.
{
std::size_t N = 10;
MyOperator<ScalarType> op(N);
Run the CG method with our on-the-fly operator. Use viennacl::linalg::bicgstab_tag() or viennacl::linalg::gmres_tag() instead of viennacl::linalg::cg_tag() to solve using BiCGStab or GMRES, respectively.
Pretty-Print solution vector to verify solution. (We use a slow direct element-access via operator[] here for convenience.)
std::cout.precision(3);
std::cout << std::fixed;
std::cout << "Result value map: " << std::endl;
std::cout << std::endl << "^ y " << std::endl;
for (std::size_t i=0; i<N; ++i)
{
std::cout << "| ";
for (std::size_t j=0; j<N; ++j)
std::cout << result[i * N + j] << " ";
std::cout << std::endl;
}
std::cout << "*---------------------------------------------> x" << std::endl;
That's it, print a completion message. Read on for details on how to implement the actual compute kernels.
std::cout << "!!!! TUTORIAL COMPLETED SUCCESSFULLY !!!!" << std::endl;
return EXIT_SUCCESS;
}
Implementation Details
So far we have only looked at the code for the control logic. In the following we define the actual 'worker' code for the matrix-free implementations.
Execution on Host
Since the execution on the host has the smallest amount of boilerplate code surrounding it, we use this case as a starting point.
template<typename NumericT>
{
NumericT const * values_x = viennacl::linalg::host_based::detail::extract_raw_pointer<NumericT>(x.
handle());
NumericT * values_y = viennacl::linalg::host_based::detail::extract_raw_pointer<NumericT>(y.
handle());
In the following we iterate over all 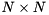 points and apply the five-point stencil directly. This is done in a straightforward manner for illustration purposes. Multi-threaded execution via OpenMP can be obtained by uncommenting the pragma below.
points and apply the five-point stencil directly. This is done in a straightforward manner for illustration purposes. Multi-threaded execution via OpenMP can be obtained by uncommenting the pragma below.
Feel free to apply additional optimizations with respect to data access patterns and the like.
for (std::size_t i=0; i<N_; ++i)
for (std::size_t j=0; j<N_; ++j)
{
NumericT value_right = (j < N_ - 1) ? values_x[ i *N_ + j + 1] : 0;
NumericT value_left = (j > 0 ) ? values_x[ i *N_ + j - 1] : 0;
NumericT value_top = (i < N_ - 1) ? values_x[(i+1)*N_ + j ] : 0;
NumericT value_bottom = (i > 0 ) ? values_x[(i-1)*N_ + j ] : 0;
NumericT value_center = values_x[i*N_ + j];
values_y[i*N_ + j] = ((value_right - value_center) / dx - (value_center - value_left) / dx) / dx
+ ((value_top - value_center) / dy - (value_center - value_bottom) / dy) / dy;
}
}
Execution via CUDA
The host-based kernel code serves as a basis for the CUDA kernel. The only thing we have to adjust are the array bounds: We assign one CUDA threadblock per index i. For a fixed i, parallelization across all threads in the block is obtained with respect to j.
Again, feel free to apply additional optimizations with respect to data access patterns and the like...
#if defined(VIENNACL_WITH_CUDA)
template<typename NumericT>
__global__
void apply_cuda_kernel(
NumericT const * values_x,
std::size_t N)
{
for (std::size_t i = blockIdx.x; i < N; i += gridDim.x)
for (std::size_t j = threadIdx.x; j < N; j += blockDim.x)
{
NumericT value_right = (j < N - 1) ? values_x[ i *N + j + 1] : 0;
NumericT value_left = (j > 0 ) ? values_x[ i *N + j - 1] : 0;
NumericT value_top = (i < N - 1) ? values_x[(i+1)*N + j ] : 0;
NumericT value_bottom = (i > 0 ) ? values_x[(i-1)*N + j ] : 0;
NumericT value_center = values_x[i*N + j];
values_y[i*N + j] = ((value_right - value_center) / dx - (value_center - value_left) / dx) / dx
+ ((value_top - value_center) / dy - (value_center - value_bottom) / dy) / dy;
}
}
#endif
#if defined(VIENNACL_WITH_CUDA)
template<typename NumericT>
{
}
#endif
Execution via OpenCL
The OpenCL kernel is almost identical to the CUDA kernel: Only a couple of keywords need to be replaced. Also, the sources need to be packed into a string:
#if defined(VIENNACL_WITH_OPENCL)
static const char * my_compute_program =
"typedef float NumericT; \n"
"__kernel void apply_opencl_kernel(__global NumericT const * values_x, \n"
" __global NumericT * values_y, \n"
" unsigned int N) {\n"
" NumericT dx = (NumericT)1 / (N + 1); \n"
" NumericT dy = (NumericT)1 / (N + 1); \n"
" for (unsigned int i = get_group_id(0); i < N; i += get_num_groups(0)) \n"
" for (unsigned int j = get_local_id(0); j < N; j += get_local_size(0)) { \n"
" NumericT value_right = (j < N - 1) ? values_x[ i *N + j + 1] : 0; \n"
" NumericT value_left = (j > 0 ) ? values_x[ i *N + j - 1] : 0; \n"
" NumericT value_top = (i < N - 1) ? values_x[(i+1)*N + j ] : 0; \n"
" NumericT value_bottom = (i > 0 ) ? values_x[(i-1)*N + j ] : 0; \n"
" NumericT value_center = values_x[i*N + j]; \n"
" values_y[i*N + j] = ((value_right - value_center) / dx - (value_center - value_left) / dx) / dx \n"
" + ((value_top - value_center) / dy - (value_center - value_bottom) / dy) / dy; \n"
" } \n"
" } \n";
#endif
Before the kernel is called for the first time, the OpenCL program containing the kernel needs to be compiled. We use a simple singleton using a static variable to achieve that.
Except for the kernel compilation at the first invocation, the OpenCL kernel launch is just one line of code just like for CUDA. Refer to custom-kernels.cpp for some more details.
#if defined(VIENNACL_WITH_OPENCL)
template<typename NumericT>
{
static bool first_run = true;
if (first_run) {
ctx.
add_program(my_compute_program,
"my_compute_program");
first_run = false;
}
}
#endif
Full Example Code
#include <iostream>
template<typename NumericT>
class MyOperator
{
public:
MyOperator(std::size_t N) : N_(N) {}
{
#if defined(VIENNACL_WITH_CUDA)
apply_cuda(x, y);
#endif
#if defined(VIENNACL_WITH_OPENCL)
apply_opencl(x, y);
#endif
apply_host(x, y);
}
std::size_t
size1()
const {
return N_ * N_; }
private:
#if defined(VIENNACL_WITH_CUDA)
#endif
#if defined(VIENNACL_WITH_OPENCL)
#endif
std::size_t N_;
};
{
std::size_t N = 10;
MyOperator<ScalarType> op(N);
std::cout.precision(3);
std::cout << std::fixed;
std::cout << "Result value map: " << std::endl;
std::cout << std::endl << "^ y " << std::endl;
for (std::size_t i=0; i<N; ++i)
{
std::cout << "| ";
for (std::size_t j=0; j<N; ++j)
std::cout << result[i * N + j] << " ";
std::cout << std::endl;
}
std::cout << "*---------------------------------------------> x" << std::endl;
std::cout << "!!!! TUTORIAL COMPLETED SUCCESSFULLY !!!!" << std::endl;
return EXIT_SUCCESS;
}
template<typename NumericT>
{
NumericT const * values_x = viennacl::linalg::host_based::detail::extract_raw_pointer<NumericT>(x.
handle());
NumericT * values_y = viennacl::linalg::host_based::detail::extract_raw_pointer<NumericT>(y.
handle());
for (std::size_t i=0; i<N_; ++i)
for (std::size_t j=0; j<N_; ++j)
{
NumericT value_right = (j < N_ - 1) ? values_x[ i *N_ + j + 1] : 0;
NumericT value_left = (j > 0 ) ? values_x[ i *N_ + j - 1] : 0;
NumericT value_top = (i < N_ - 1) ? values_x[(i+1)*N_ + j ] : 0;
NumericT value_bottom = (i > 0 ) ? values_x[(i-1)*N_ + j ] : 0;
NumericT value_center = values_x[i*N_ + j];
values_y[i*N_ + j] = ((value_right - value_center) / dx - (value_center - value_left) / dx) / dx
+ ((value_top - value_center) / dy - (value_center - value_bottom) / dy) / dy;
}
}
#if defined(VIENNACL_WITH_CUDA)
template<typename NumericT>
__global__
void apply_cuda_kernel(
NumericT const * values_x,
std::size_t N)
{
for (std::size_t i = blockIdx.x; i < N; i += gridDim.x)
for (std::size_t j = threadIdx.x; j < N; j += blockDim.x)
{
NumericT value_right = (j < N - 1) ? values_x[ i *N + j + 1] : 0;
NumericT value_left = (j > 0 ) ? values_x[ i *N + j - 1] : 0;
NumericT value_top = (i < N - 1) ? values_x[(i+1)*N + j ] : 0;
NumericT value_bottom = (i > 0 ) ? values_x[(i-1)*N + j ] : 0;
NumericT value_center = values_x[i*N + j];
values_y[i*N + j] = ((value_right - value_center) / dx - (value_center - value_left) / dx) / dx
+ ((value_top - value_center) / dy - (value_center - value_bottom) / dy) / dy;
}
}
#endif
#if defined(VIENNACL_WITH_CUDA)
template<typename NumericT>
{
}
#endif
#if defined(VIENNACL_WITH_OPENCL)
static const char * my_compute_program =
"typedef float NumericT; \n"
"__kernel void apply_opencl_kernel(__global NumericT const * values_x, \n"
" __global NumericT * values_y, \n"
" unsigned int N) {\n"
" NumericT dx = (NumericT)1 / (N + 1); \n"
" NumericT dy = (NumericT)1 / (N + 1); \n"
" for (unsigned int i = get_group_id(0); i < N; i += get_num_groups(0)) \n"
" for (unsigned int j = get_local_id(0); j < N; j += get_local_size(0)) { \n"
" NumericT value_right = (j < N - 1) ? values_x[ i *N + j + 1] : 0; \n"
" NumericT value_left = (j > 0 ) ? values_x[ i *N + j - 1] : 0; \n"
" NumericT value_top = (i < N - 1) ? values_x[(i+1)*N + j ] : 0; \n"
" NumericT value_bottom = (i > 0 ) ? values_x[(i-1)*N + j ] : 0; \n"
" NumericT value_center = values_x[i*N + j]; \n"
" values_y[i*N + j] = ((value_right - value_center) / dx - (value_center - value_left) / dx) / dx \n"
" + ((value_top - value_center) / dy - (value_center - value_bottom) / dy) / dy; \n"
" } \n"
" } \n";
#endif
#if defined(VIENNACL_WITH_OPENCL)
template<typename NumericT>
{
static bool first_run = true;
if (first_run) {
ctx.
add_program(my_compute_program,
"my_compute_program");
first_run = false;
}
}
#endif
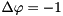 on the unit square
on the unit square ![$ [0,1] \times [0,1] $](form_139.png) with homogeneous Dirichlet boundary conditions using a finite-difference discretization. A
with homogeneous Dirichlet boundary conditions using a finite-difference discretization. A 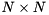 grid is used, where the first and the last points per dimensions represent the boundary. For simplicity we only consider the host-backend here. Have a look at custom-kernels.hpp and custom-cuda.cu on how to use custom kernels in such a matrix-free setting.
grid is used, where the first and the last points per dimensions represent the boundary. For simplicity we only consider the host-backend here. Have a look at custom-kernels.hpp and custom-cuda.cu on how to use custom kernels in such a matrix-free setting.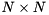 grid for solving Poisson's equation. It only holds the number of grid points per coordinate direction and implements the
grid for solving Poisson's equation. It only holds the number of grid points per coordinate direction and implements the 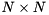 points and apply the five-point stencil directly. This is done in a straightforward manner for illustration purposes. Multi-threaded execution via OpenMP can be obtained by uncommenting the pragma below.
points and apply the five-point stencil directly. This is done in a straightforward manner for illustration purposes. Multi-threaded execution via OpenMP can be obtained by uncommenting the pragma below.