The basic types have been introduced in the previous chapter, so we move on with the description of the basic BLAS operations. Almost all operations supported by Boost.uBLAS are available, including element-wise operations on vectors. Thus, consider the Boost.uBLAS documentation as a reference as well.
ViennaCL provides all vector-vector operations defined at level 1 of BLAS as well as the most important element-wise operations:
| Verbal | Mathematics | ViennaCL Code |
|---|---|---|
| swap |  | swap(x,y); |
| stretch |  | x *= alpha; |
| assignment |  | y = x; |
| multiply add | 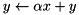 | y += alpha * x; |
| multiply subtract | 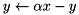 | y -= alpha * x; |
| inner dot product | 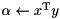 | inner_prod(x,y); |
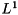 norm norm | 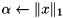 | alpha = norm_1(x); |
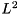 norm norm | 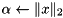 | alpha = norm_2(x); |
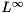 norm norm |  | alpha = norm_inf(x); |
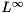 norm index norm index | 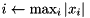 | i = index_norm_inf(x); |
| plane rotation | 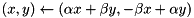 | plane_rotation(a, b, x, y); |
| elementwise product | 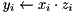 | y = element_prod(x,z); |
| elementwise division | 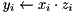 | y = element_div(x,z); |
| elementwise power |  | y = element_pow(x,z); |
| elementwise modulus (ints) | 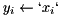 | y = element_abs(x); |
| elementwise modulus (floats) | 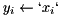 | y = element_fabs(x); |
| elementwise acos | 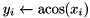 | y = element_acos(x); |
| elementwise asin | 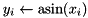 | y = element_asin(x); |
| elementwise atan |  | y = element_atan(x); |
| elementwise ceil |  | y = element_ceil(x); |
| elementwise cos |  | y = element_cos(x); |
| elementwise cosh | 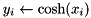 | y = element_cosh(x); |
| elementwise exp |  | y = element_exp(x); |
| elementwise floor |  | y = element_floor(x); |
| elementwise log (base e) | 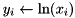 | y = element_log(x); |
| elementwise log (base 10) | 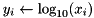 | y = element_log10(x); |
| elementwise sin |  | y = element_sin(x); |
| elementwise sinh | 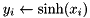 | y = element_sinh(x); |
| elementwise sqrt |  | y = element_sqrt(x); |
| elementwise tan |  | y = element_tan(x); |
| elementwise tanh | 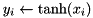 | y = element_tanh(x); |
BLAS level 1 routines mapped to ViennaCL. Note that the free functions reside in namespace viennacl::linalg
The function interface is compatible with Boost.uBLAS, thus allowing quick code migration for Boost.uBLAS users. Element-wise operations and standard operator overloads are available for dense matrices as well. The only dense matrix norm provided is norm_frobenius() for the Frobenius norm.
auto for the result type, as this might result in unexpected performance regressions or dangling references.The interface for level 2 BLAS functions in ViennaCL is similar to that of Boost.uBLAS:
| Verbal | Mathematics | ViennaCL Code |
|---|---|---|
| matrix vector product |  | y = prod(A, x); |
| matrix vector product | 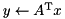 | y = prod(trans(A), x); |
| inplace mv product | 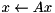 | x = prod(A, x); |
| inplace mv product | 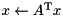 | x = prod(trans(A), x); |
| scaled product add | 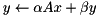 | y = alpha * prod(A, x) + beta * y |
| scaled product add |  | y = alpha * prod(trans(A), x) + beta * y |
| tri. matrix solve |  | y = solve(A, x, tag); |
| tri. matrix solve | 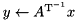 | y = solve(trans(A), x, tag); |
| inplace solve |  | inplace_solve(A, x, tag); |
| inplace solve |  | inplace_solve(trans(A), x, tag); |
| rank 1 update | 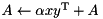 | A += alpha * outer_prod(x,y); |
| symm. rank 1 update |  | A += alpha * outer_prod(x,x); |
| rank 2 update | 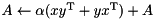 | A += alpha * outer_prod(x,y); A += alpha * outer_prod(y,x); |
BLAS level 2 routines mapped to ViennaCL. Note that the free functions reside in namespace viennacl::linalg.
tag is one out of lower_tag, unit_lower_tag, upper_tag, and unit_upper_tag.
auto for the result type, as this might result in unexpected performance regressions or dangling references.While BLAS levels 1 and 2 are mostly memory-bandwidth-limited, BLAS level 3 is mostly limited by the available computational power of the respective device. Hence, matrix-matrix products regularly show impressive performance gains on mid- to high-end GPUs when compared to a single CPU core (which is apparently not a fair comparison...)
Again, the ViennaCL API is identical to that of Boost.uBLAS and comparisons can be carried out immediately, as is shown in the tutorial located in examples/tutorial/blas3.cpp.
As for performance, ViennaCL yields decent performance gains at BLAS level 3 on mid- to high-end GPUs. However, highest performance is usually obtained only with careful tuning to the respective target device. ViennaCL provides kernels that are device-specific and thus achieve high efficiency, without sacrificing the portability of OpenCL. Best performance is usually obtained with the OpenCL backend. The CUDA backend provides good performance for NVIDIA GPUs. The OpenMP backend, however, currently provides only moderate performance and is not recommended for BLAS level 3 operations (as well as algorithms depending on them).
| Verbal | Mathematics | ViennaCL |
|---|---|---|
| matrix-matrix product | 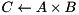 | C = prod(A, B); |
| matrix-matrix product | 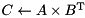 | C = prod(A, trans(B)); |
| matrix-matrix product |  | C = prod(trans(A), B); |
| matrix-matrix product | 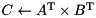 | C = prod(trans(A), trans(B)); |
| tri. matrix solve |  | C = solve(A, B, tag); |
| tri. matrix solve |  | C = solve(trans(A), B, tag); |
| tri. matrix solve |  | C = solve(A, trans(B), tag); |
| tri. matrix solve | 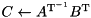 | C = solve(trans(A), trans(B), tag); |
| inplace solve | 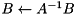 | inplace_solve(A, trans(B), tag); |
| inplace solve | 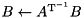 | inplace_solve(trans(A), x, tag); |
| inplace solve |  | inplace_solve(A, trans(B), tag); |
| inplace solve | 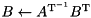 | inplace_solve(trans(A), x, tag); |
BLAS level 3 routines mapped to ViennaCL. Note that the free functions reside in namespace viennacl::linalg
auto for the result type, as this might result in unexpected performance regressions or dangling references.The most important operation on sparse matrices is the sparse matrix-vector product, available for all sparse matrix types in ViennaCL. An example for compressed_matrix<T> is as follows:
For best performance we recommend compressed_matrix<T>, hyb_matrix<T>, or sliced_ell_matrix<T>. Unfortunately it is not possible to predict the fastest matrix type in general, thus a certain amount of trial-and-error by the library user is required.
Have a look at the ViennaCL Benchmark Section for a performance comparison of sparse matrix-vector products for different storage formats.
Several graph algorithms or multigrid methods require the multiplication of two sparse matrices. ViennaCL provides an implementation based on the row-merge algorithm developed by Gremse et al. for NVIDIA GPUs [15]. We extended the row-merge algorithm and derived high-performance implemented for CPUs, OpenCL-enabled GPUs from AMD, and INTEL's Xeon Phi. The calling code, however, remains as simple as possible:
Have a look at the ViennaCL Benchmark Section for a performance comparison of sparse matrix-matrix products.
compressed_matrix<T>. Other sparse matrix formats do not allow for a high-performance implementation.For many algorithms it is of interest to extract a single row or column of a dense matrix, or to access the matrix diagonal. This is provided in the same way as for Boost.uBLAS through the free functions row(), column(), and diag():
The function diag can also be used to create a matrix which has the provided vector entries in the off-diagonal:
This is similar to MATLAB's diag() function.
Operations such as the vector operation x = y + z; in ViennaCL require that the numeric type (i.e. the first template parameter for the type) is the same. Thus, it is not possible to e.g. mix single-precision floating point vectors with integer vectors within the same operation. However, it is possible to convert vectors and dense matrices by direct assignment. An example code snippet for vectors is as follows: