This chapter provides a brief overview of the basic interfaces and usage of the provided data types. Operations on the various types are explained in Basic Operations.

Scalar Type

The scalar type scalar<T> with template parameter T denoting the underlying CPU scalar type (char, short, int, long, float and double, if supported - see table of supported hardware) and represents single scalar value on the computing device. scalar<T> is designed to behave much like a scalar type on conventional host-based CPU processing, but library users have to keep in mind that every operation on scalar<T>| may require the launch of an appropriate compute kernel on the GPU, thus making the operation much slower then the conventional CPU equivalent. Even if the host-based computing backend of ViennaCL is used, some (small) overheads occur.

Note: Be aware that operations between objects of type scalar<T> (e.g.~additions, comparisons) have large overhead on GPU backends. A separate compute kernel launch is required for every operation in such case.

Example Usage

The scalar type of ViennaCL can be used just like the built-in types, as the following snippet shows:

float cpu_float = 42.0f;
double cpu_double = 13.7603;
viennacl::scalar<float>  gpu_float(3.1415f);
viennacl::scalar<double> gpu_double = 2.71828;
//conversions
cpu_float = gpu_float;
gpu_float = cpu_double;  //automatic transfer and conversion
cpu_float = gpu_float * 2.0f;
cpu_double = gpu_float - cpu_float;

Mixing built-in types with the ViennaCL scalar is usually not a problem. Nevertheless, since every operation requires OpenCL calls, such arithmetics should be used sparsingly.

Note: It is not possible to assign a scalar<float> to a scalar<double> directly.; Mixing operations between objects of different scalar types is not supported. Convert the data manually on the host if needed.

Members

Apart from suitably overloaded operators that mimic the behavior of the respective CPU counterparts, only a single public member function handle() is available:

Interface	Comment
`v.handle()`	The memory handle (CPU, CUDA, or OpenCL)

Interface of scalar<T> in ViennaCL. Destructors and operator overloads for BLAS are not listed.

Vector Type

The main vector type in ViennaCL is vector<T, alignment>, representing a chunk of memory on the compute device. T is the underlying scalar type (char, short, int, long, float, or double if supported, - see table of supported hardware). Complex types are not supported in ViennaCL. The second template argument alignment is deprecated and should not be specified by the library user.

At construction, vector<T, alignment> is initialized to have the supplied length and the memory is initialized to zero (similar to std::vector<T>). A difference to CPU implementations is that accessing single vector elements is very costly, because every time an element is accessed, it has to be transferred from the CPU to the compute device or vice versa.

Example Usage

The following code snippet shows the typical use of the vector type provided by ViennaCL. The overloaded function copy(), which is used similar to std::copy() from the C++ Standard Template Library (STL), should be used for writing vector entries:

std::vector<ScalarType>      stl_vec(10);
viennacl::vector<ScalarType> vcl_vec(10);
//fill the STL vector:
for (size_t i=0; i<stl_vec.size(); ++i)
  stl_vec[i] = i;
//copy content to GPU vector (recommended initialization)
copy(stl_vec.begin(), stl_vec.end(), vcl_vec.begin());
//manipulate GPU vector here
//copy content from GPU vector back to STL vector
copy(vcl_vec.begin(), vcl_vec.end(), stl_vec.begin());

The function copy() does not assume that the values of the supplied CPU object are located in a linear memory sequence. If this is the case, the function fast_copy provides better performance.

Once the vectors are set up on the GPU, they can be used like objects on the CPU (refer to Basic Operations for more details):

// let vcl_vec1 and vcl_vec2 denote two vector on the GPU
vcl_vec1 *= 2.0;
vcl_vec2 += vcl_vec1;
vcl_vec1 = vcl_vec1 - 3.0 * vcl_vec2;

Members

At construction, vector<T, alignment> is initialized to have the supplied length, but memory is not initialized. If initialization is desired, the memory can be initialized with zero values using the member function clear(). Other member functions are as follows:

Interface	Comment
`CTOR(n)`	Constructor with number of entries
`v(i)`	Access to the `i`-th element of v (slow for GPUs!)
`v[i]`	Access to the `i`-th element of v (slow for GPUs!)
`v.clear()`	Initialize v with zeros
`v.resize(n, bool preserve)`	Resize v to length n. Preserves old values if bool is true.
`v.begin()`	Iterator to the begin of the matrix
`v.end()`	Iterator to the end of the matrix
`v.size()`	Length of the vector
`v.swap(v2)`	Swap the content of v with v2
`v.internal_size()`	Returns the number of entries allocated on the GPU (taking alignment into account)
`v.empty()`	Shorthand notation for `v.size() == 0`
`v.clear()`	Sets all entries in v to zero
`v.handle()`	Returns the memory handle (needed for custom kernels, see Custom Compute Kernels)

Interface of vector<T> in ViennaCL. Destructors and operator overloads for BLAS are not listed.

Note: Accessing single elements of a vector using operator() or operator[] is very slow for GPUs due to PCI-Express latency! Use with care!

One important difference to pure CPU implementations is that the bracket operator as well as the parenthesis operator are very slow, because for each access an OpenCL data transfer has to be initiated. The overhead of this transfer is orders of magnitude. For example:

// fill a vector on CPU
for (size_t i=0; i<cpu_vector.size(); ++i)
  cpu_vector(i) = 1e-3f;
// fill a ViennaCL vector - VERY SLOW with GPU backends!!
for (size_t i=0; i<gpu_vector.size(); ++i)
  vcl_vector(i) = 1e-3f;

The difference in execution speed is typically several orders of magnitude, therefore direct vector element access should be used only if a very small number of entries is accessed in this way. A much faster initialization is as follows:

// fill a vector on CPU
for (long i=0; i<cpu_vector.size(); ++i)
  cpu_vector(i) = 1e-3f;
// fill a vector on GPU with data from CPU - faster versions:
copy(cpu_vector, vcl_vector);                                   //option 1
copy(cpu_vector.begin(), cpu_vector.end(), vcl_vector.begin()); //option 2

In this way, setup costs for the CPU vector and the ViennaCL vector are comparable.

Dense Matrix Type

matrix<T, F, alignment> represents a dense matrix. The second optional template argument F specifies the storage layout and defaults to row_major. As an alternative, a column_major memory layout can be used. The third template argument alignment denotes an alignment for the rows and columns for row-major and column-major memory layout and should no longer be specified by the user (cf. alignment for the vector type).

Memory layout of a row-major dense matrix. The rows and columns of the matrix may be padded, such that the internal buffer is of size `internal_size1()*internal_size2()` elements.

Note: For efficiency purposes, the rows and columns of matrices in ViennaCL may be padded by additional zeros.

Example Usage

The use of matrix<T, F> is similar to that of the counterpart in Boost.uBLAS. The operators are overloaded similarly.

//set up a 3 by 5 matrix:
viennacl::matrix<float>  vcl_matrix(4, 5);
//fill it up:
vcl_matrix(0,2) = 1.0;
vcl_matrix(1,2) = -1.5;
vcl_matrix(2,0) = 4.2;
vcl_matrix(3,4) = 3.1415;

Note: Accessing single elements of a matrix using operator() is very slow on GPU backends! Use with care!

A much better way is to initialize a dense matrix using the provided copy() function:

//copy content from CPU matrix to GPU matrix
copy(cpu_matrix, gpu_matrix);
//copy content from GPU matrix to CPU matrix
copy(gpu_matrix, cpu_matrix);

The type requirement for a class instantiated in an object cpu_matrix is thatoperator() can be used for accessing entries, that a member function size1() returns the number of rows and that size2() returns the number of columns. Please refer to Interfacing Other Libraries for an overview of other libraries for which an overload of copy() is provided.

Note: The internal memory buffer of a matrix<> is by default padded with zeros so that the internal matrix size is a multiple of e.g. a power of two.; When using fast_copy() on a matrix, the padded zeros need to be taken into account correctly. Query internal_size1() and internal_size2() to do so.

Members

The members are as follows, with the usual operator overloads not listed explicitly:

Interface	Comment
`CTOR(nrows, ncols)`	Constructor with number of rows and columns
`mat(i,j)`	Access to the element in the `i`-th row and the `j`-th column of `mat`
`mat.resize(m, n, bool preserve)`	Resize mat to m rows and n columns. Currently, the boolean flag is ignored and entries always discarded.
`mat.size1()`	Number of rows in mat
`mat.internal_size1()`	Internal number of rows in mat
`mat.size2()`	Number of columns in mat
`mat.internal_size2()`	Internal number of columns in mat
`mat.clear()`	Sets all entries in v to zero
`mat.handle()`	Returns the memory handle (needed for custom kernels, see Custom Compute Kernels)

Interface of the dense matrix type matrix<T, F> in ViennaCL. Constructors, Destructors and operator overloads for BLAS are not listed.

Initializer Types

Note: Initializer types in ViennaCL can currently only be used for initializing vectors and matrices, not for computations!

In order to initialize vectors, the following initializer types are provided, again similar to Boost.uBLAS:

`unit_vector<T>(s, i)`	Unit vector of size with entry at index , zero elsewhere.
`zero_vector<T>(s)`	Vector of size with all entries being zero.
`scalar_vector<T>(s, v)`	Vector of size with all entries equal to .
`random_vector<T>(s, d)`	Vector of size with all entries random according to the distribution specified by .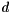

For example, to initialize a vector v1 with all $ 42 $ entries being $ 42.0 $ , use

viennacl::vector<float> v1 = viennacl::scalar_vector<float>(42, 42.0f);

Similarly the following initializer types are available for matrices:

`identity_matrix<T>(s)`	Identity matrix of dimension $s \times s$ .
`zero_matrix<T>(s1, s2)`	Matrix of size $s_1 \times s_2$ with all entries being zero.
`scalar_matrix<T>(s1, s2, v)`	Matrix of size $s_1 \times s_2$ with all entries equal to .
`random_matrix<T>(s1, s2, d)`	Vector of size with all entries random according to the distribution specified by .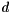

Sparse Matrix Types

Several different sparse matrix types are provided in ViennaCL, which will be discussed in the following.

Compressed Matrix

compressed_matrix<T, alignment> represents a sparse matrix using a compressed sparse row (CSR) scheme, for which a sparse matrix-vector multiplication kernel based on CSR-adaptive [14] is available. T is the floating point type. alignment is the alignment and defaults to 1 at present. In general, sparse matrices should be set up on the CPU and then be pushed to the compute device using copy(), because dynamic memory management of sparse matrices is not provided on OpenCL compute devices such as GPUs.

Interface	Comment
`CTOR(nrows, ncols)`	Constructor with number of rows and columns
`mat.set()`	Initialize mat with the data provided as arguments
`mat.reserve(num)`	Reserve memory for up to `num` nonzero entries
`mat.size1()`	Number of rows in `mat`
`mat.size2()`	Number of columns in `mat`
`mat.nnz()`	Number of nonzeroes in `mat`
`mat.resize(m, n, bool preserve)`	Resize mat to `m` rows and `n` columns. Currently, the boolean flag is ignored and entries always discarded.
`mat.handle1()`	Returns the memory handle holding the row indices (needed for custom kernels, see Custom Compute Kernels)
`mat.handle2()`	Returns the memory handle holding the column indices (needed for custom kernels, see Custom Compute Kernels)
`mat.handle()`	Returns the memory handle holding the entries (needed for custom kernels, see Custom Compute Kernels)

Interface of the sparse matrix type compressed_matrix<T, F> in ViennaCL. Destructors and operator overloads for BLAS are not listed.

Example Usage

The use of compressed_matrix<T, alignment> is similar to that of the counterpart in Boost.uBLAS. The operators are overloaded similarly. There is a direct interfacing with the standard implementation using a vector of maps from the STL:

//set up a sparse 3 by 5 matrix on the CPU:
std::vector< std::map< unsigned int, float> > cpu_sparse_matrix(4);
//fill it up:
cpu_sparse_matrix[0][2] =  1.0;
cpu_sparse_matrix[1][2] = -1.5;
cpu_sparse_matrix[3][0] =  4.2;
//set up a sparse ViennaCL matrix:
viennacl::compressed_matrix<float>  vcl_sparse_matrix(4, 5);
//copy to OpenCL device:
copy(cpu_sparse_matrix, vcl_sparse_matrix);
//copy back to CPU:
copy(vcl_sparse_matrix, cpu_sparse_matrix);

The copy() functions can also be used with a generic sparse matrix data type fulfilling the following requirements:

The const_iterator1 type is provided for iteration along increasing row index
The const_iterator2 type is provided for iteration along increasing column index
.begin1() returns an iterator pointing to the element with indices (0,0).
.end1() returns an iterator pointing to the end of the first column
When copying to the cpu type: Write operation via operator()
When copying to the cpu type: resize(m,n,preserve) member (cf. Table of members)

The iterator returned from the cpu sparse matrix type via begin1() has to fulfill the following requirements:

.begin() returns an column iterator pointing to the first nonzero element in the particular row.
.end() returns an iterator pointing to the end of the row
Increment and dereference

For the sparse matrix types in Boost.uBLAS, these requirements are all fulfilled. Please refer to Interfacing Other Libraries for an overview of other libraries for which an overload of copy() is provided.

Members

The interface is described in Table of members.

Coordinate Matrix

In the second sparse matrix type, coordinate_matrix<T, alignment>, entries are stored as triplets (i,j,val), where i is the row index, j is the column index, and val is the entry. T is the floating point type. The optional alignment defaults to 128 at present and should not be provided by the user. In general, sparse matrices should be set up on the CPU and then be pushed to the compute device using copy(), because dynamic memory management of sparse matrices is not provided on OpenCL compute devices such as GPUs.

Interface	Comment
`CTOR(nrows, ncols)`	Constructor with number of rows and columns
`mat.reserve(num)`	Reserve memory for `num` nonzero entries
`mat.size1()`	Number of rows in `mat`
`mat.size2()`	Number of columns in `mat`
`mat.nnz()`	Number of nonzeroes in `mat`
`mat.resize(m, n, bool preserve)`	Resize `mat` to `m` rows and `n` columns. Currently, the boolean flag is ignored and entries always discarded.
`mat.resize(m, n)`	Resize mat to `m` rows and `n` columns. Does not preserve old values.
`mat.handle12()`	Returns the memory handle holding the row and column indices (needed for custom kernels, see Custom Compute Kernels)
`mat.handle()`	Returns the memory handle holding the entries (needed for custom kernels, see Custom Compute Kernels)

Interface of the sparse matrix type coordinate_matrix<T, A> in ViennaCL. Destructors and operator overloads for BLAS operations are not listed.

Example Usage

The use of coordinate_matrix<T, alignment> is similar to that of the first sparse matrix type compressed_matrix<T, alignment>, thus we refer to the example usage of compressed_matrix<>.

Members

The interface is described in this table.

Note: Note that only a few preconditioners work with coordinate_matrix so far.

ELL Matrix

A sparse matrix in ELL format of type ell_matrix is stored in a block of memory of size $N \times n_{\max}$ , where N is the number of rows of the matrix and $n_{\max}$ is the maximum number of nonzeros per row. Rows with less than $n_{\max}$ entries are padded with zeros. In a second memory block, the respective column indices are stored.

The ELL format is well suited for matrices where most rows have approximately the same number of nonzeros. This is often the case for matrices arising from the discretization of partial differential equations using e.g. the finite element method. On the other hand, the ELL format introduces substantial overhead if the number of nonzeros per row varies a lot.

For an example use of an ell_matrix, have a look at examples/benchmarks/sparse.cpp.

Note: Note that preconditioners do not work with ell_matrix yet.

Sliced ELL Matrix

A variation of the ELL format was recently proposed by Kreutzer et al. for use on CPUs, GPUs, and Intel's MIC architecture. The implementation in ViennaCL does not reorder the rows of the matrix, but is otherwise as proposed in the paper.

For an example use of sliced_ell_matrix, have a look at examples/benchmarks/sparse.cpp.

Note: Note that preconditioners do not work with sliced_ell_matrix yet.

Hybrid Matrix

The higher performance of the ELL format for matrices with approximately the same number of entries per row and the higher flexibility of the CSR format is combined in the hyb_matrix type, where the main part of the system matrix is stored in ELL format and excess entries are stored in CSR format.

For an example use of an hyb_matrix, have a look at examples/benchmarks/sparse.cpp.

Note: Note that preconditioners do not work with hyb_matrix yet.

Compressed Compressed Matrix

If only a few rows of a sparse matrix are populated, then the previous sparse matrix formats are fairly expensive in terms of memory consumption. This is addressed by the compressed_compressed_matrix<> format, which is similar to the standard CSR format, but only stores the rows containing nonzero elements. An additional array is used to store the global row index r in the sparse matrix A of the i-th nonzero row.

Note: Note that preconditioners do not work with compressed_compressed_matrix yet.

Proxies

Similar to Boost.uBLAS, ViennaCL provides range and slice objects in order to conveniently manipulate dense submatrices and vectors. The functionality is provided in the headers viennacl/vector_proxy.hpp and viennacl/matrix_proxy.hpp respectively. A range refers to a contiguous integer interval and is set up as

std::size_t lower_bound = 1;
std::size_t upper_bound = 7;
viennacl::range r(lower_bound, upper_bound);

A slice is similar to a range and allows in addition for arbitrary increments (stride). For example, to create a slice consisting of the indices 2, 5, 8, 11, 14, use the code

std::size_t start  = 2;
std::size_t stride = 3;
std::size_t size   = 5
viennacl::slice s(start, stride, size);

In order to address a subvector of a vector v and a submatrix of a matrix M, the proxy objects v_sub and M_sub are created as follows:

typedef viennacl::vector<ScalarType>                      VectorType;
typedef viennacl::matrix<ScalarType, viennacl::row_major> MatrixType;
viennacl::vector_range<VCLVectorType> v_sub(v, r);
viennacl::matrix_range<VCLMatrixType> M_sub(M, r, r);

As a shortcut, one may use the free function project() in order to avoid having to write the type explicitly:

project(v, r);    //returns a vector_range as above
project(M, r, r); //returns a matrix_range as above

In the same way a vector_slice and a matrix_slice are set up.

The proxy objects can now be manipulated in the same way as vectors and dense matrices. In particular, operations such as vector proxy additions and matrix additions work as usual, e.g.

vcl_sub += vcl_sub; //or project(v, r) += project(v, r);
M_sub   += M_sub;   //or project(M, r, r) += project(M, r, r);

Submatrix-Submatrix products are computed in the same manner and are handy for many block-based linear algebra algorithms.

Example code can be found in examples/tutorial/vector-range.cpp and examples/tutorial/matrix-range.cpp